Research
The overarching objective of my research is to establish provably safe performance capabilities for nonlinear systems under significant uncertainties. My Ph.D. thesis mainly involves developing a novel control algorithm called Reachable Predictive Control (RPC) that is capable of navigating to a provably reachable state while avoiding unsafe regions without knowledge of the system dynamics. The novelty of this method is the lack of information needed to implement it. That is, RPC can effectively follow piecewise linear trajectories in real time without relying on a dynamics model or prior data for offline system identification. In contrast, control methods require a physics-based model for implementation and provide sluggish performance once uncertainty passes a threshold; neural networks require training data to train a model offline and cannot be implemented onboard without prior relevant data.
Ideal applications include the autonomous control of air and space systems under abrupt changes in their dynamics due to adverse events, as well as the control of chaotic systems, such as soft robots, where existing models are notoriously inadequate for achieving high-performance autonomy. To demonstrate the algorithm's efficacy, I am currently applying RPC onto an autonomous vehicle with the objective of successfully navigating around obstacles to reach some final state within a theoretically guaranteed time frame without the use of a dynamics model.
Reachable Predictive Control: A Novel Algorithm for the Control of Unknown Nonlinear Systems without a Dynamics Model
The RPC control algorithm pipeline is presented below:
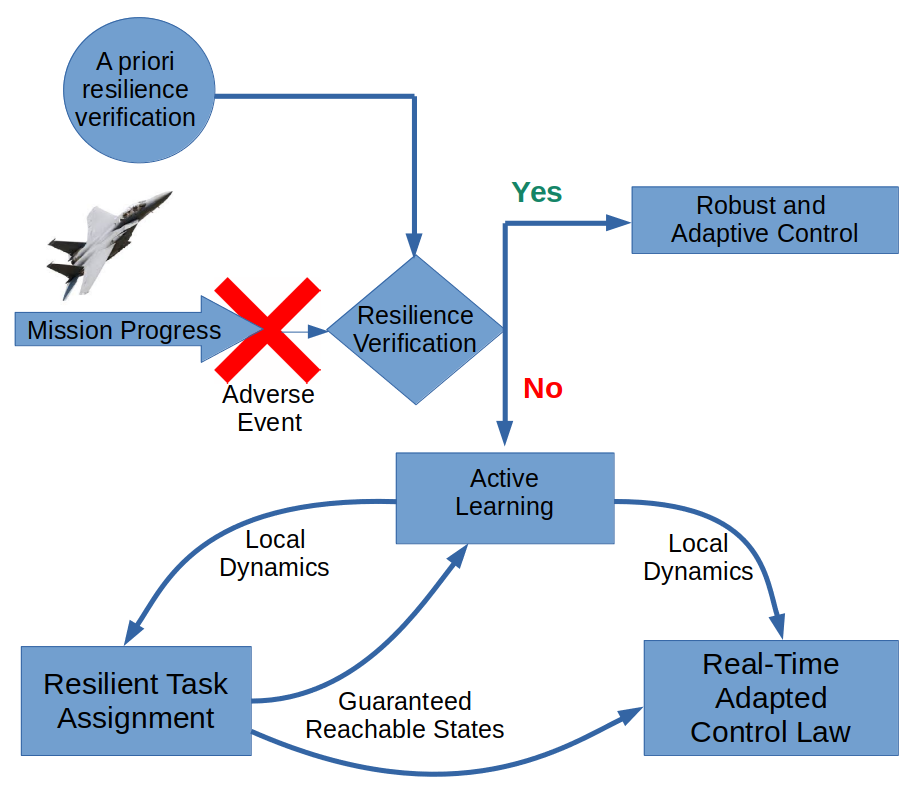
RPC works as follows: (1) Resilience Verification: determine if current robust and adaptive control methods would provide sufficient autonomous capabilities to achieve the control objective; if not, (2) Active Learning: execute a learning cycle to learn the dynamics locally; (3) Resilient Task Assignment: determine a guaranteed set of reachable states without knowledge of the system dynamics; (4) Controller Synthesis: synthesize control action based on the limited knowledge from active learning and resilient task assignment; (5) repeat steps (2)-(4) to iteratively navigate to a provably reachable location without knowledge of the true system dynamics. Below is a list of relevant publications for RPC.
Active Learning: Resilient Task Assignment:- Reachability of Nonlinear Systems with Unknown Dynamics
- Maximal Ellipsoid Method for Guaranteed Reachability of Unknown Fully Actuated Systems
- Guaranteed Reachability on Riemannian Manifolds for Unknown Nonlinear Systems
- Identifying Single Input Linear System Dynamics from Reachable Sets
- Online Learning and Control Synthesis for Reachable Paths of Unknown Nonlinear Systems
We consider nonlinear control-affine systems of the form $$\dot{x} = f(x) + G(x)u,\quad x(0) = x_0$$ where $u\in\mathbb{B}^m(0;1)$ and $f, G$ are unknown and represent the drift and the control input vector field respectively. When implementing RPC, the system initially undergoes a learning cycle where m+1 excitations to its actuators provide the local dynamics around $x = x_0$. That is, the system can determine $f(x_0)$ and $G(x_0)$, however $f(x)$ and $G(x)$ for $x \neq x_0$ still remain unknown. Then, the system performs resilient task assignment, where it will autonomously determine a set of states that are reachable for all systems which satisfy (i) the local dynamics from active learning, and (ii) the growth rate on the bounds of those dynamics gathered from known physical laws -- the following reference is provided for additional background on reachability analysis. We refer to this underapproximated set as the Guaranteed Reachable Set (GRS), which naturally translates to a set of states we can provably reach within a given timeframe without knowledge of the system dynamics.
If we are given a set of states to reach over a period of time, we can use this information to form reachable paths to follow. We thus aim to characterize the GRS to determine reachable paths for autonomous navigation. A path is tightly connected to the notion of velocities. That is, a path can be thought of as a set of velocities at each point on the path, so intuitively, we start by finding an underapproximation of the set of all attainable velocities, then use that information to form the GRS. We provide an illustration of resilient task assignment below.
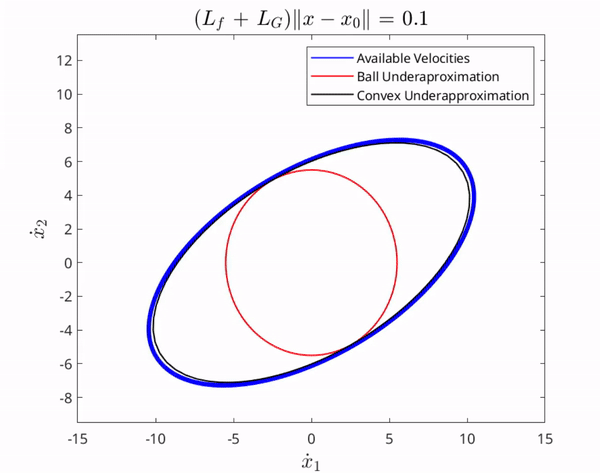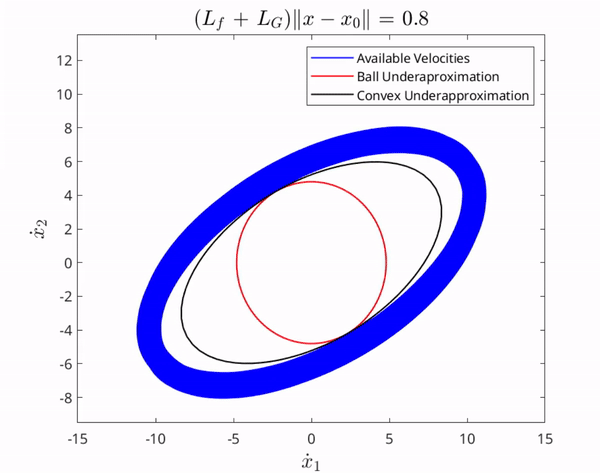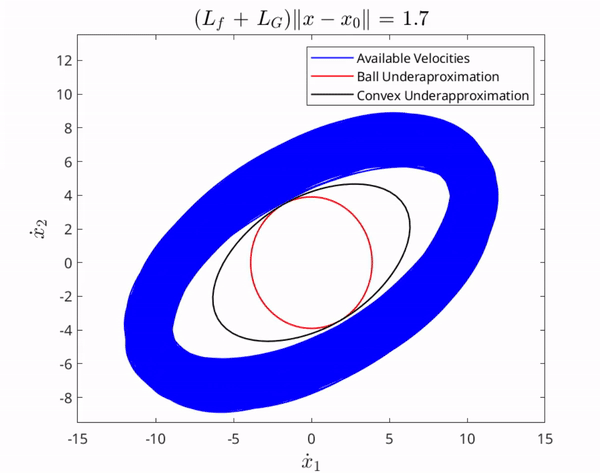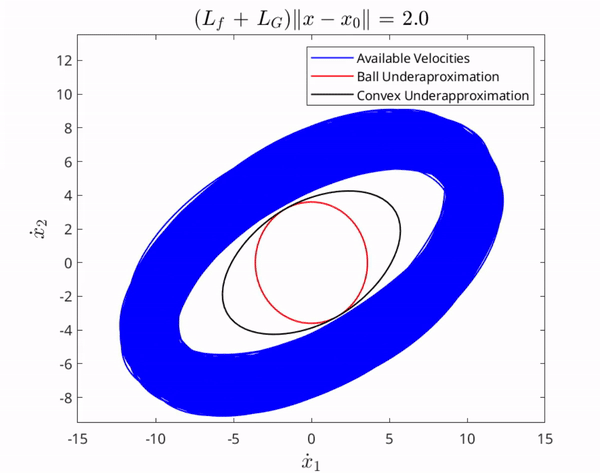
The set of velocities attainable by all $f,G$ consistent with our assumptions is in the interior of the blue region. The red and black sets are underapproximations contained in this interior for all time.
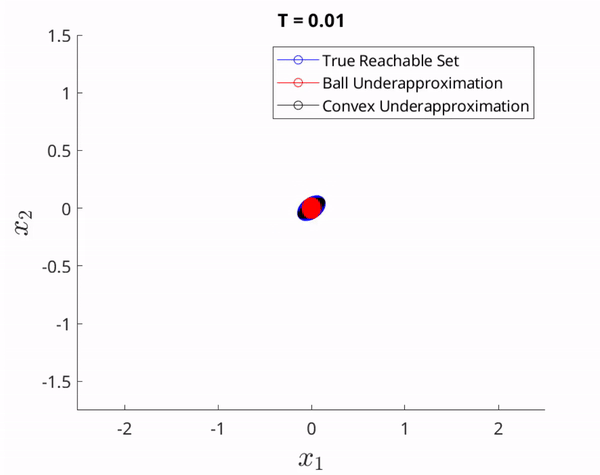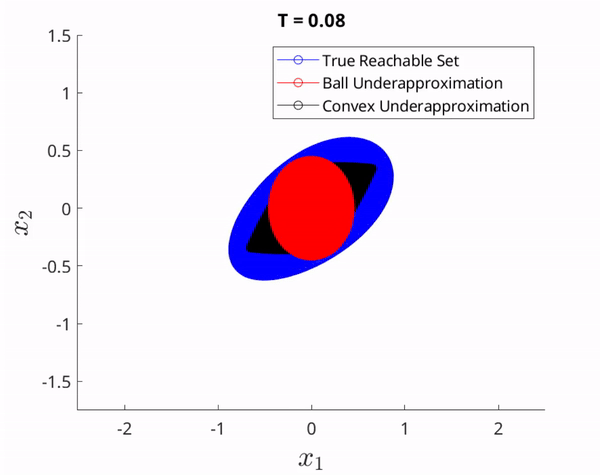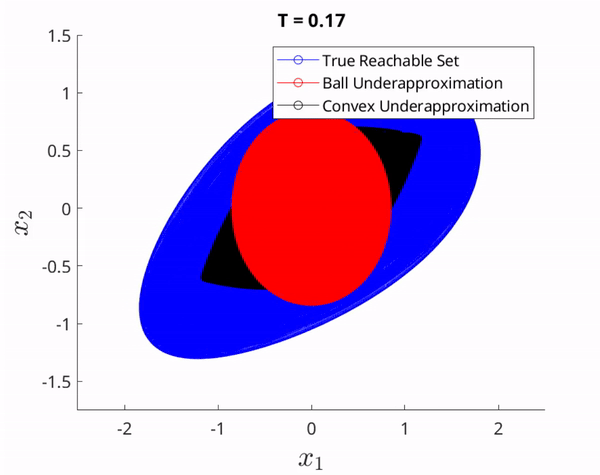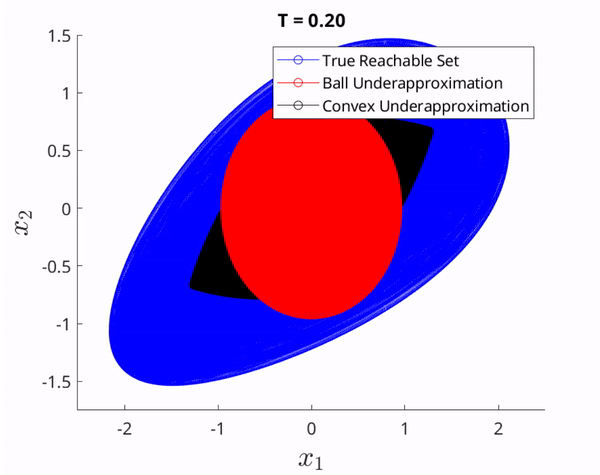
The set of guaranteed reachable states corresponding to the set of attainable velocities in the GVS. The red and black sets in the GVS correspond to the red and black sets which form the union of all paths that can be followed from $x_0$.
Notice in the figures above that since the red and black sets are contained it the GVS, their corresponding paths are contained in the unknown nonlinear system's true reachable set. We emphasize that without knowledge of the unknown nonlinear system dynamics, the true reachable set is impossible to calculate in general cases, and thus we aim to underapproximate it to isolate a set of reachable paths.
Intuitively, the larger the set contained within the underapproximation of the GVS, the larger the set of states we can provably reach, and thus the more paths we can navigate to. This motivates us to try and maximize the volume of the set contained within the GVS. We discuss in this paper how, in the case of nonlinear control-affine systems, this problem is mathematically equivalent to characterizing a set contained in the interior of an intersection of infinitely many ellipses and we formally prove a way to find a maximally inscribed ellipsoid contained in the intersection of infinitely many ellipsoid, thus resulting in an optimal underapproximation.
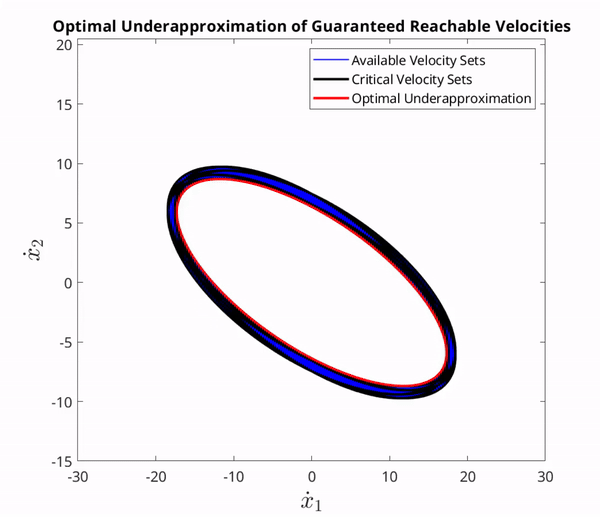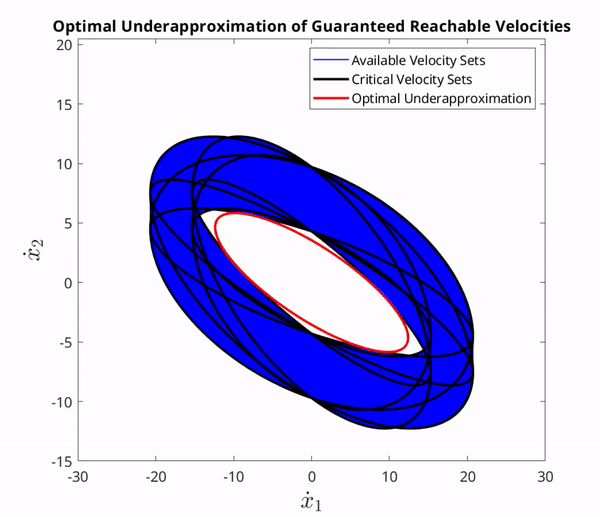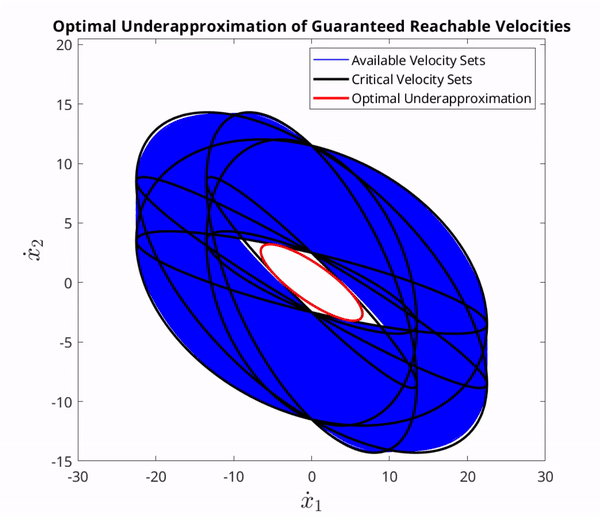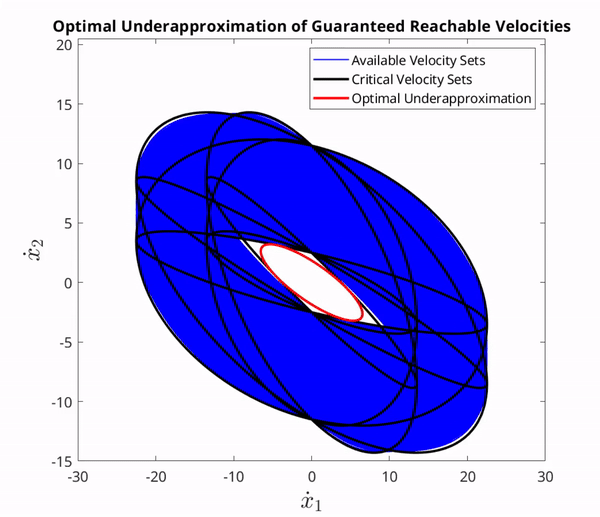
An optimal underapproximation of the GVS as time increases. The optimization was performed using MATLAB's MOSEK optimization toolbox.
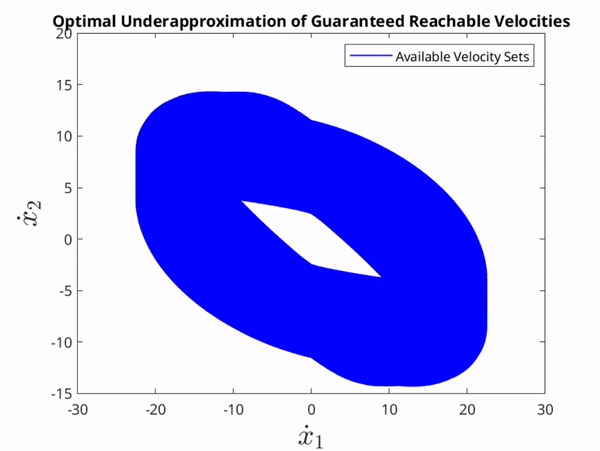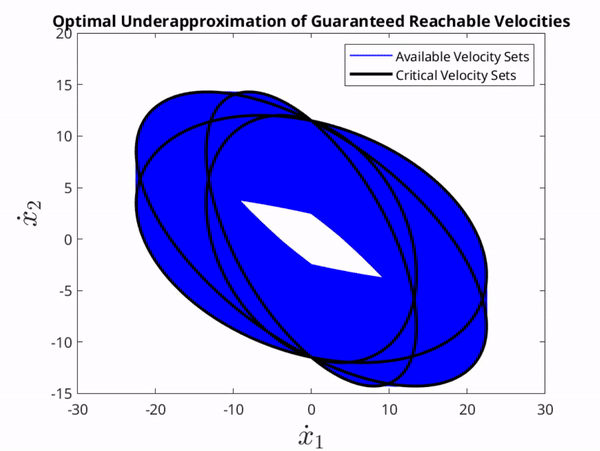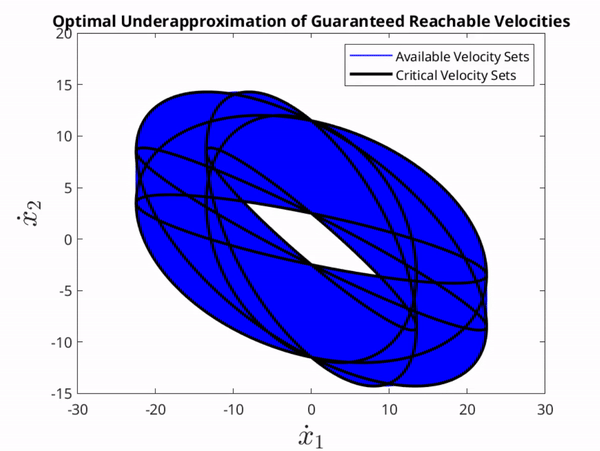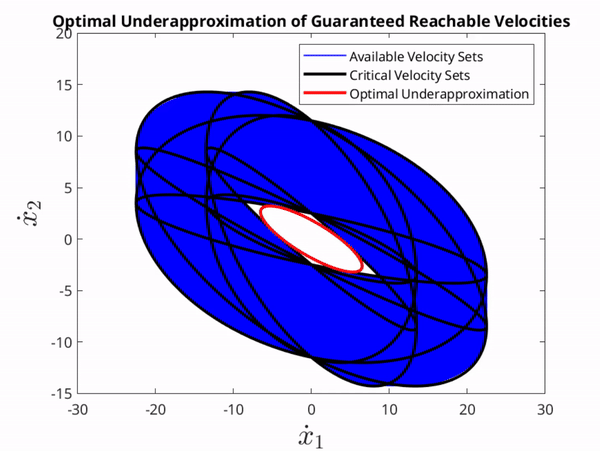
The set of critical ellipses used at a single time instance to underaproximate the GVS and the corresponding optimal set.
It is generally impossible to solve an optimization problem with infinitely many constraints. As a result, this paper aimed primarily to show how this same interior could be characterized by finitely many ellipoids, which we refer to as critical velocity sets in the figure above. We can use these sets to solve a finite optimization problem using methods in Convex Optimization by Boyd, hence resulting in an optimal solution. These results were also recently generalized to any system existing on complete Riemannian manifolds for improved capabilities and a wider range of practical applications.
With the implementation of advanced optimization and geometric methods, resilient task assignment is sufficiently developed enough to provide the information we need for controller synthesis. Existing publications pertaining to controller synthesis detail how we can: (1) use reachable sets to uniquely determine the system dynamics of an unknown system and (2) synthesize control action using theoretical guarantees from resilient task assignment. Current efforts build on (2), where we use the set of reachable states from resilient task assignment to synthesize control action. Below is an illustration of RPC following a desired path confirmed reachable through resilient task assignment. Specifically, efforts focus on implementing Reachable Predictive Control to navigate an autonomous vehicle around obstacles to a desired target state within a theoretically guaranteed amount of time without the use of the vehicle's dynamics model.
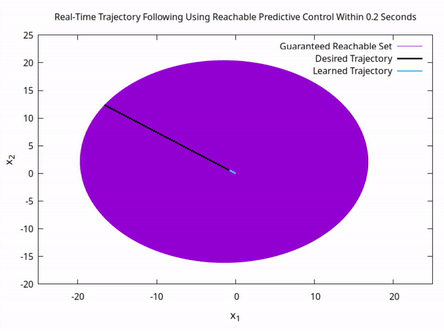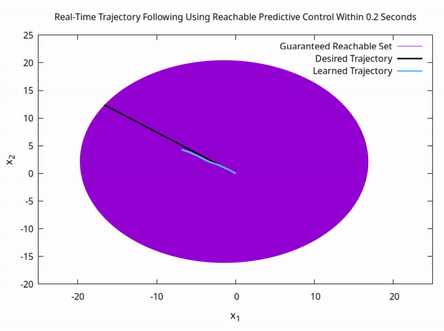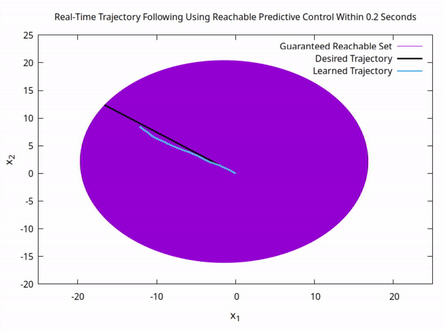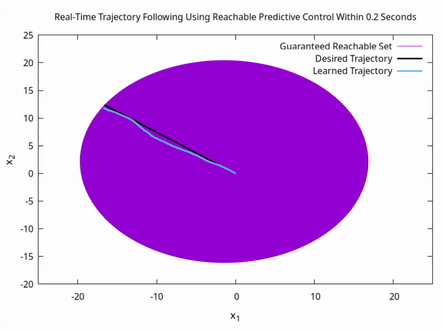
Control action is synthesized onboard to follow a linear trajectory towards a state on the boundary of the guaranteed reachable set (GRS) of an unknown system. The GRS is calculated for T = 0.2 seconds while the control action is fully synthesized in 0.1895 seconds.
We demonstrate how RPC can use waypoint navigation to navigate to some state that is not within the immediate viscinity of the system's initial location $x_0$. This is possible by calculating the GRS at some initial condition, following a path to a desired state, and then reinitializing the terminal state as its new initial condition. This process is repeated, causing the system to follow waypoints until some desired final state is reached. Thoeretical guarantees in this paper prove that the algorithm can track any desired trajectory by converging to the terminal state while remaining within a bounded radius of the followed path.
Below is a video demonstrating autonomous waypoint navigation of a straight path. The picture on the left is zoomed-in to demonstrate in detail the path following capabilities of RPC within a convergent radius, while a zoomed-out video shows that, despite the minor oscillations, the path is closely followed to a sufficient degree.
With waypoint navigation capabilities, RPC is ready to be appied onto an autonomous vehicle. Inspired by "the floor is lava", we show that the car can avoid unsafe regions while following a narrow, veering path safely to its final destination. Observe the input and state plots on the bottom left and right respectively. The input plot shows how RPC inputs learn optimal controls during execution. The state plot illustrates the algorithm's ability to calculate guaranteed steering capabilities to correctly judge whether it can execute a turn in time given its current velocity. The algorithm then uses this information to successfully avoid the lava while making turns and reaching its destination.